2967.
Unification day
Byteland has n cities, but no one road. The king of
the country, Waldemar de Bear, decided to remedy this situation, he wants to
connect some cities with roads so that along these roads it will be possible to
reach any city from any other city. When construction will be completed, the
king plans to celebrate the Unification Day.
Unfortunately,
the treasury in Byteland is almost empty, so the king needs to save money and
minimize the total length of constructed roads.
Input. The first
line contains the number n (1 ≤ n ≤ 5000) of cities in Byteland. Each
of the next n lines contains two
integers xi, yi, the coordinates of i-th city (-10000 ≤ xi, yi ≤ 10000). No two cities are located
in one point.
Output. Print the
least total roads length. Print the answer with the accuracy no less
than 10-3.
|
Sample
input |
Sample
output |
|
6 1 1 7 1 2 2 6 2 1 3 7 3 |
9.6568542495 |
SOLUTION
graphs – minimum spanning tree – Prim
Algorithm analysis
To solve the
problem, you need to find the minimum spanning tree (MST). Implement Prim algorithm.
Example
Construct the minimum spanning tree
for the graph given in the sample.
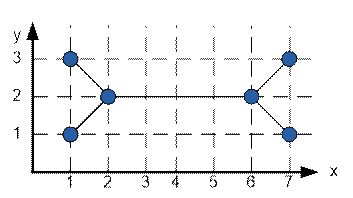
The weight of the minimum spanning tree is 4 + 4![]() ≈ 9.65.
≈ 9.65.
Algorithm realization
Declare global
arrays. Store the coordinates of the cities in (x[i], y[i]).
used[i] = 1, if vertex i is included in MST.
#define MAX 5001
#define INF 0x3F3F3F3F
int x[MAX], y[MAX];
int used[MAX], dist[MAX];
The
function dist2 computes the squared distance
between cities i and j.
int dist2(int i, int j)
{
return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);
}
Function Prim implements the Prim’s
algorithm and returns the value of MST.
double Prim(void)
{
Initialize the arrays.
memset(dist, 0x3F, sizeof(dist));
memset(used, 0, sizeof(used));
Start to construct the MST from the vertex 0. Initialize
dist[0] = 0, used[0] = 1. In the variable res
compute the size of MST.
double res = 0;
int i, j, cur = 0;
dist[cur] = 0;
used[cur] = 1;
Make n – 1 iterations. At each iteration,
add one vertex to MST (so n – 1 vertices should
be added to MST).
for (i = 1; i < n; i++)
{
The current vertex is cur. Iterate over the
edges (cur, j) and recalculate the value of dist[j].
Thus dist[j] stores the current shortest distance from vertex j to
the current MST.
for (j = 0; j < n; j++)
if
(!used[j] && (dist2(cur, j) < dist[j]))
dist[j] = dist2(cur, j);
Find the shortest edge that will be included in MST. To
do this, look for the smallest dist[j] such that the
vertex j does not yet belong to MST (used[j]
= 0). The number of the vertex with the smallest dist[j] is stored into cur (it
becomes the current one).
int min = INF;
for (j = 0; j < n; j++)
if
(!used[j] && (dist[j] < min))
{
min = dist[j];
cur = j;
}
Vertex cur is included to MST. The edge of
length sqrt(dist[cur]) is
added to MST.
used[cur] = 1;
res += sqrt(dist[cur]);
}
return res;
}
The main part of the program. Read the input data.
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%d %d", &x[i], &y[i]);
Run the Prim’s algorithm and print the answer.
res =
Prim();
printf("%lf\n", res);
Algorithm realization –
min_e / end_e
Declare the arrays. Store
the city coordinates in (x[i], y[i]).
#define MAX
5001
int
x[MAX], y[MAX];
int
used[MAX], min_e[MAX], end_e[MAX];
The function dist2 computes the squared distance between cities i and j.
int
dist2(int i, int
j)
{
return (x[j] -
x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);
}
The main part of the program. Read the coordinates of the cities.
scanf("%d",&n);
for(i =
0; i < n; i++)
scanf("%d
%d",&x[i], &y[i]);
Initialize the arrays.
memset(min_e,0x3F,sizeof(min_e));
memset(end_e,-1,sizeof(end_e));
memset(used,0,sizeof(used));
The size of MST will be calculated in the dist variable.
dist =
min_e[1] = 0;
for (i =
0; i < n; i++)
{
Look for the vertex v with
minimum value of min_e[v] among the vertices that
are not yet included in MST (for which used[v]
= 0).
v = -1;
for (j = 0; j
< n; j++)
if
(!used[j] && (v == -1 || min_e[j] < min_e[v])) v = j;
Include the vertex v into MST.
Add an edge (v, end_e[v]) to MST.
used[v] = 1;
if (end_e[v]
!= -1) dist += sqrt((double)dist2(v,end_e[v]));
Recompute the labels for the edges outgoing from v.
for (to = 0;
to < n; to++)
{
int dV_TO =
dist2(v,to);
if
(!used[to] && (dV_TO < min_e[to]))
{
min_e[to] = dV_TO;
end_e[to] = v;
}
}
}
Print the value of MST.
printf("%.6lf\n",dist);
Java realization
import java.util.*;
public class Main
{
static int x[], y[];
static int used[], min_e[], end_e[];
static int dist2(int i, int j)
{
return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
x = new int[n];
y = new int[n];
for(int i = 0; i < n; i++)
{
x[i] = con.nextInt();
y[i] = con.nextInt();
}
min_e = new int[n];
Arrays.fill(min_e, Integer.MAX_VALUE);
end_e = new int[n];
Arrays.fill(end_e, -1);
used = new int[n];
double dist = min_e[1] = 0;
for (int i = 0; i < n; i++)
{
int v = -1;
for (int j = 0; j < n; j++)
if (used[j] == 0 && (v == -1 || min_e[j] < min_e[v])) v = j;
used[v] = 1;
if (end_e[v] != -1)
dist += Math.sqrt((double)dist2(v,end_e[v]));
for (int to = 0; to < n; to++)
{
int dV_TO = dist2(v,to);
if (used[to] == 0 && (dV_TO < min_e[to]))
{
min_e[to] = dV_TO;
end_e[to] = v;
}
}
}
System.out.println(dist);
con.close();
}
}